Числа Фибоначчи
Чи́сла Фибона́ччи — элементы числовой последовательности
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS)
в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (или Фибоначчи).
Более формально, последовательность чисел Фибоначчи ![]() задается рекуррентным соотношением:
задается рекуррентным соотношением:
![]()
Иногда числа Фибоначчи рассматривают и для неположительных номеров n как двусторонне бесконечную последовательность, удовлетворяющую основному соотношению. Члены с такими номерами легко получить с помощью эквивалентной формулы «назад»: Fn = Fn + 2 − Fn + 1:
|
n |
-10 |
-9 |
-8 |
-7 |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Fn |
-55 |
34 |
-21 |
13 |
-8 |
5 |
-3 |
2 |
-1 |
1 |
0 |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
Легко видеть, что F − n = ( − 1)n + 1Fn. Для чисел Фибоначчи с отрицательными индексами остаются верными большинство нижеприведённых свойств.
Формула Бине
Формула Бине выражает в явном виде значение Fn как функцию от n:
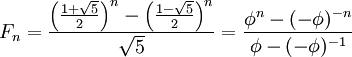 ,
,
где ![]() — золотое сечение. При этом
— золотое сечение. При этом ![]() и
и ![]() являются корнями квадратного уравнения
являются корнями квадратного уравнения ![]() .
.
Из формулы Бине следует, что для всех ![]() , Fn есть ближайшее к
, Fn есть ближайшее к ![]() целое число, то есть
целое число, то есть 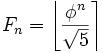 . В частности, справедлива асимптотика
. В частности, справедлива асимптотика![]() .
.
- Числа Фибоначчи представляются значениями континуант на наборе единиц:
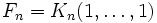 , то есть
, то есть
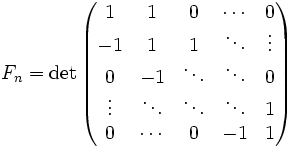 , а также
, а также 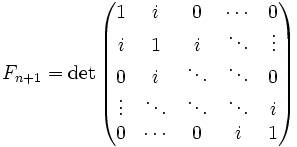 ,
,
где матрицы имеют размер ![]() , i — мнимая единица.
, i — мнимая единица.
- Числа Фибоначчи можно выразить через многочлены Чебышёва:
![]()
![]()
- Для любого n,
![]()
· Следствие. Подсчёт определителей даёт
![]()
- Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е. (Fm,Fn) = F(m,n). Следствия:
- Fm делится на Fn тогда и только тогда, когда m делится на n (за исключением n = 2). В частности, Fm делится на F3 = 2 (то есть является чётным) только для m = 3k; Fm делится на F4 = 3 только для m = 4k; Fm делится на F5 = 5 только для m = 5k и т. д.
- Fm может быть простым только для простых m (с единственным исключением m = 4) (например, число 233 простое, и индекс его, равный 13, также прост). Обратное не верно, первый контрпример —
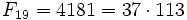 . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
. Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
- Последовательность чисел Фибоначчи является частным случаем возвратной последовательности, её характеристический многочлен x2 - x - 1имеет корни
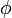 и
и 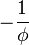 .
.
- Отношения
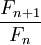 являются подходящими дробями золотого сечения φ и, в частности,
являются подходящими дробями золотого сечения φ и, в частности, 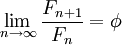 .
. - Суммы биномиальных коэффициентов на диагоналях треугольника Паскаля являются числами Фибоначчи ввиду формулы
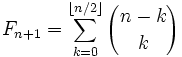 .
.
- В 1964 Дж. Кон (J. H. E. Cohn) доказал, что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12: F0 = 02 = 0, F1 = 12 = 1, F2 = 12 = 1, F12 = 122 = 144. При этом для n=0,1,12 верно утверждение Fn = n2.
- Производящей функцией последовательности чисел Фибоначчи является:
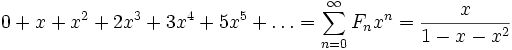
- Множество чисел Фибоначчи совпадает с множеством положительных значений многочлена
z(x,y) = 2xy4 + x2y3 − 2x3y2 − y5 − x4y + 2y,
на множестве неотрицательных целых чисел x и y.
- Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
- Последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом 60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом 300, последние три цифры — с периодом 1500, последние четыре — с периодом 15000, последние пять — с периодом 150000 и т.д.
- Числа трибоначчи
- Числа Фибоначчи являются частным случаем последовательностей Люка
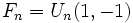 , при этом их дополнением являются числа Люка
, при этом их дополнением являются числа Люка 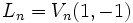 .
.
Число прочтений: 23110
| Посетитель | Комментарий |
|---|---|
вася |
18.10.12 16:Oct:th |
| Этог что за бред? |
|
Наталья |
17.02.15 12:Feb:th |
| В 1989 году я закончила НИСКТ (Новосибирский Институт Советской Кооперативной Торговли). На практических занятиях преподаватель по финансам дал нам одну универсальную формулу. В дальнейшем я по ней сделала расчёт, перспектива развития своего предприятия, где работала на тот момент, включила в курсовую работу. Получилось, что в 1992 году прибыль предприятия упадёт ниже ноля. Преподаватель курса Рынков возмутилась, спросила какую формулу я использовала. Курсовую попросила переписать. А эту курсовую - отдать ей. Как послушный гражданин я так и сделала. По предприятию в 1992 году, как сами понимаете, мой прогноз сбылся. Тетрадь, где была формула пропала, а курсовая была в других руках. С тех пор я ищу, какая эта была формула. Так как преподаватель по Финансам дал формулу на примере, в лекциях я её не нашла. Предполагаю, что это формула Фибоначчи. Тождества напоминают мои расчёты в курсовой. Вот так получив образование, имея на руках лекции, я не воспользовалась тем, что могло бы повлиять на всю мою жизнь в лучшую сторону. Кстати, по этой формуле ранее я делала расчёты по своей дате рождения, критические периоды. Совпадения в семье есть. Та ли эта формула, которую я искала? | |
Фибоначчер |
01.10.16 02:Oct:st |
| Привет, ихтеандры! | |
Вячеслав |
06.05.18 14:May:th |
| в 5 тождестве ошибка: написано:"=(-1)^n+1", а должно быть: "=(-1)^n" | |